Standaardafwijking: wat is het en hoe bereken je het?
Standaardafwijking: wat is het en hoe bereken je het?
Standaardafwijking of standaarddeviatie zegt iets over hoe verschillende getallen in een waarneming verspreid zijn.
Hoe reken je dit precies uit en kan dit ook met je rekenmachine? Mr. Chadd legt het je uit.

Deviatie
De standaardafwijking (σ) zegt iets over hoe ver getallen in een verdeling van het gemiddelde af zitten. De formule hiervoor is:
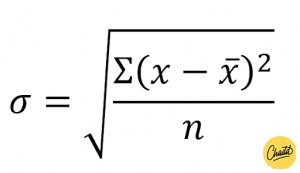
Hieronder volgt een stappenplan hoe je de standaardafwijking kunt uitrekenen.
- Je moet hiervoor eerst de deviatie uitrekenen. De formule voor deviatie is: d = x – x̄. Hierbij is x̄ het gemiddelde en x de waarde van een individuele meting.
- Om de standaardafwijking te berekenen, moet je vervolgens alle deviaties kwadrateren en bij elkaar optellen (het Σ-teken in de formule betekent dat je de waarden bij elkaar optelt).
- Vervolgens deel je dit door het aantal waarnemingen (dit is n in de formule).
- Als laatste trek je de wortel van dit hele getal en dan heb je de standaardafwijking gevonden.
Bijvoorbeeld: je hebt een sample met de waarden 7, 3, 8. Het gemiddelde hiervan is (7+3+8)/3 = 6. De deviaties zijn dan d = 7 – 6 = 1 , d = 3 – 6 = -3 en d = 8 – 6 = 2 .
Vervolgens moet je deze waarden kwadrateren en optellen, dus 12 + (-3)2 + 22 = 1 + 9 + 4 = 14. Je moet dit aantal vervolgens delen door het aantal waarnemingen, dus 14/3 = 4,667. De laatste stap is de wortel hiervan √4,667 = 2,160.
Kan je toch nog wel wat extra hulp gebruiken? Onze coaches kunnen jou ook 1-op-1 helpen! Check hier onze bijlespagina voor meer informatie!
Zo werkt de app
Rekenmachine
Je kunt dit ook uitrekenen op je grafische rekenmachine. Je moet hiervoor eerst je waarnemingsgetallen invullen met 1-Var Stats (TI) of 1VAR (Casio). Nadat je dit hebt gedaan, kun je de optie σx gebruiken (zowel Casio als TI) om de standaardafwijking te berekenen. De optie 1-Var Stats of 1VAR vind je als je naar STAT gaat en vervolgens naar CALC. Je krijgt dan een lijstje te zien met alle waarden, waaronder de standaarddeviatie.
Oefenvraag
Wat is de standaarddeviatie van de volgende waarneming?
1, 3, 5, 6, 8, 9?
Leerlingen die hier vragen over hebben, keken ook naar:
Werkt u in het vo of mbo? Plan direct een vrijblijvende demonstratie in!
We laten u graag geheel vrijblijvend zien hoe Mr. Chadd werkt, hoe het kan worden ingezet en wat de meerwaarde is. Dit doen we in een fysieke of online afspraak van zo'n 30 minuten. Let op! Deze demonstratie is alleen bedoeld voor mensen die werkzaam zijn in het vo of mbo, NIET voor leerlingen!

Meer informatie over Mr. Chadd
Laat hieronder uw gegevens achter en we sturen u geheel vrijblijvend meer informatie over Mr. Chadd op!

Werkt u in het vo of mbo? Neem contact op!
Bent u benieuwd naar de voordelen van Mr. Chadd of heeft u andere vragen? Laat uw gegevens achter en wij nemen zo snel mogelijk contact op.

